نگاهی (طولانی) به یادگیری تقویتی – بخش اول

متن زیر ترجمه A (Long) Peek into Reinforcement Learning است.

چند خبر هیجان انگیز در زمینه هوش مصنوعی (AI) به تازگی در سال های اخیر اتفاق افتاده است. AlphaGo بهترین بازیکن حرفه‌ای انسان را در بازی Go شکست داد. خیلی زود الگوریتم توسعه یافته AlphaGo Zero بدون یادگیری نظارتی بر پایه دانش بشری، AlphaGo را ۱۰۰-۰ شکست داد.

بازیکنان حرفه‌ای برتر بازی از ربات توسعه یافته توسط OpenAI در مسابقات یک به یک DOTA2 شکست خوردند. پس از دانستن این موارد، کنجکاو نبودن در مورد جادوی پشت این الگوریتم‌ها یعنی یادگیری تقویتی (RL)، بسیار سخت است. من این پست را می نویسم تا به طور خلاصه به این زمینه بپردازم. ابتدا چندین مفهوم اساسی را معرفی می‌کنیم و سپس به رویکردهای کلاسیک برای حل مسائل RL می‌پردازیم. امیدواریم که این پست بتواند نقطه شروع خوبی برای تازه‌کاران باشد، و پل ارتباطی برای مطالعه آینده بر روی تحقیقات پیشرفته باشد.

یادگیری تقویتی چیست؟

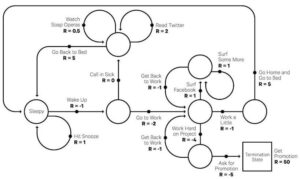
فرض کنید، ما یک عامل در یک محیط ناشناخته داریم و این عامل می‌تواند با تعامل با محیط، پاداش‌هایی را به دست آورد. عامل، باید اقداماتی را انجام دهد تا پاداش‌های انباشته را به حداکثر برساند. در واقعیت، این سناریو می‌تواند یک ربات باشد که یک بازی را برای دستیابی به امتیازات بالا انجام می‌دهد، یا یک ربات که تلاش می‌کند وظایف فیزیکی را با آیتم‌های فیزیکی کامل کند؛ و فقط به اینها محدود نمی شود.

هدف یادگیری تقویتی (RL) آموختن یک استراتژی خوب به عامل از طریق آزمایشات تجربی و بازخورد نسبی ساده دریافت شده است. با استراتژی بهینه، عامل قادر است به طور فعال با محیط سازگار شود تا پاداش های آینده را به حداکثر برساند.

مفاهیم کلیدی

حال اجازه دهید به طور رسمی مجموعه‌ای از مفاهیم کلیدی در RL را تعریف کنیم.

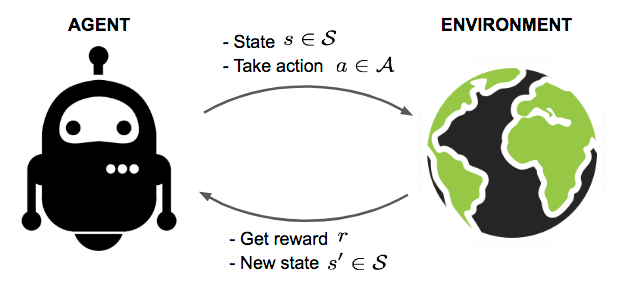
عامل در یک محیط عمل می‌کند. نحوه واکنش محیط به اقدامات خاص توسط مدلی تعریف می‌شود که ممکن است ما بشناسیم یا نشناسیم. عامل می‌تواند در یکی از چندین حالت (s ∈ S) از محیط باشد، و انجام یکی از اقدامات متعدد (a ∈ A) برای تغییر وضعیت از یک حالت به حالت دیگر را انتخاب کند. اینکه عامل به کدام حالت خواهد رسید با احتمالات انتقال بین حالت‌ها (P) تعیین می‌شود. هنگامی که یک اقدام انجام می‌شود، محیط یک پاداش (r ∈ R) به عنوان بازخورد ارائه می کند.

مدل تابع پاداش و احتمالات انتقال را تعریف می‌کند. ما ممکن است ندانیم یا ندانیم که مدل چگونه کار می‌کند و این دو شرایط را متمایز ایجاد می‌کند:

• مدل را می‌شناسیم: برنامه‌ریزی با اطلاعات کامل. RL مبتنی بر مدل را انجام دهید. هنگامی که محیط را کاملاً بشناسیم، می‌توانیم راه‌حل بهینه را با برنامه نویسی پویا (DP) پیدا کنیم. آیا هنوز "طولانی ترین دنباله رو به افزایش" یا "مشکل فروشنده دوره گرد" را از کلاس الگوریتم ۱۰۱ خود به یاد دارید؟ روده بر شدن از خنده. گرچه این موضوع تمرکز این پست نیست.
• مدل را نمی‌شناسیم : یادگیری با اطلاعات ناقص. RL بدون مدل را انجام دهید یا سعی کنید مدل را به طور صریح به عنوان بخشی از الگوریتم یاد بگیرید. بسیاری از مطالب زیر  سناریوهایی را در زمانی که مدل ناشناخته است ارائه می‌کنند.

خط مشی عامل π (s) رهنمودی را در مورد اینکه چه اقدامی بهینه برای انجام در یک وضعیت خاص با هدف به حداکثر رساندن مجموع پاداش ها است، ارائه می‌دهد. هر حالت با یک تابع مقدار V (s)مرتبط است میزان مورد انتظار پاداش‌های آینده که می‌توانیم در این حالت با اعمال سیاست مربوطه دریافت کنیم را پیش‌بینی می‌کند. به عبارت دیگر، تابع مقدار، میزان خوب بودن یک حالت را کمی می‌کند. هر دو تابع خط مشی و ارزش چیزی هستند که ما سعی می‌کنیم در یادگیری تقویتی بیاموزیم.

تعامل بین عامل و محیط شامل توالی از اقدامات و پاداش‌های مشاهده شده در زمان است t = 1 , 2 , … , T. عامل در طول فرآیند، دانش در مورد محیط را جمع‌آوری می‌کند، خط مشی بهینه را می‌آموزد، و تصمیم می‌گیرد که کدام اقدام بعدی را انجام دهد تا به طور موثر بهترین خط مشی را بیاموزد. بیایید وضعیت، عمل، و پاداش در مرحله زمانی t را به ترتیب به عنوان S t، A t و R tبرچسب گذاری کنیم. بنابراین توالی تعامل به طور کامل توسط یک قسمت توصیف می شود (همچنین به عنوان "آزمایش" یا "مسیر" شناخته می‌شود) و دنباله در حالت پایانی S T به پایان می‌رسد.

S 1 , A 1 , R 2 , S 2 , A 2 , … , S T

عباراتی که هنگام کارکردن در دسته‌های مختلف الگوریتم‌های RL با آنها زیاد مواجه خواهید شد:

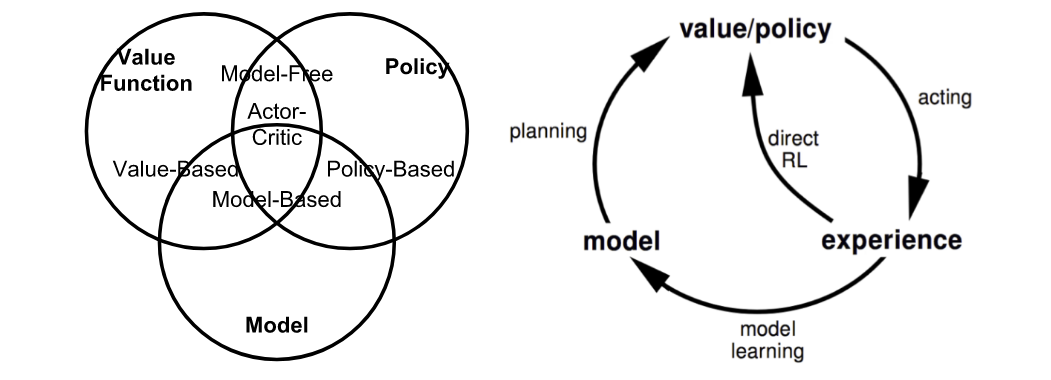
• مبتنی بر مدل: بر مدل محیط تکیه می‌کند؛ یا مدل شناخته شده است یا الگوریتم آن را به صراحت یاد می‌گیرد.
• بدون مدل: بدون وابستگی به مدل در طول یادگیری.
• بر اساس خط مشی : از نتایج قطعی یا نمونه‌هایی از خط مشی هدف برای آموزش الگوریتم استفاده می‌کند.
• خارج از خط مشی : آموزش بر روی یک توزیع از انتقال‌ها یا قسمت‌های تولید شده توسط یک خط مشی رفتاری متفاوت به جای آنچه توسط خط مشی هدف تولید می‌شود.

مدل: انتقال و پاداش

مدل توصیف کننده محیط است. با مدل، می‌توانیم یاد بگیریم یا استنباط کنیم که چگونه محیط با عامل تعامل می‌کند و به آن بازخورد ارائه می‌کند. مدل دارای دو بخش عمده است، تابع احتمال انتقال P

و تابع پاداش R.

فرض کنید وقتی در حالت s هستیم، تصمیم می‌گیریم برای رسیدن به حالت بعدی s' و دریافت پاداش r، اقدامی را انجام دهیم. این به عنوان یک مرحله انتقال شناخته می‌شود که با یک تاپل (s، a، s'، r) نشان داده می‌شود.

تابع انتقال P احتمال انتقال از حالت s به s' را پس از انجام اقدام و در حین دریافت پاداش r ثبت می‌کند. ما از Pبه عنوان نماد "احتمال" استفاده می‌کنیم.

P ( s ′ , r | s , a ) = P [ S t + 1 = s ′ , R t + 1 = r | S t = s , A t = a ]

بنابراین تابع حالت-انتقال را می‌توان به عنوان تابعی از P ( s ′ , r | s , a ) تعریف کرد:

P s s ′ a = P ( s ′ | s , a ) = P [ S t + 1 = s ′ | S t = s , A t = a ] = ∑ r ∈ R P ( s ′ , r | s , a )

تابع پاداش R پاداش بعدی ناشی از یک عمل را پیش بینی می‌کند:

R ( s , a ) = E [ R t + 1 | S t = s , A t = a ] = ∑ r ∈ R r ∑ s ′ ∈ S P ( s ′ , r | s , a )

خط مشی

خط مشی، به عنوان تایع π رفتار عامل، به ما می گوید که در حالت s کدام اقدام را انجام دهیم. این یک نقشه برداری از حالت s به عمل a است و می تواند قطعی یا تصادفی باشد:

• قطعی: π ( s ) = a
• تصادفی: π ( a | s ) = P π [ A = a | S = s ].

تابع ارزش

تابع ارزش با پیش‌بینی پاداش آینده، خوبی یک حالت یا میزان پاداش یک حالت یا یک عمل را اندازه‌ گیری می‌کند. پاداش آینده که به عنوان بازده نیز شناخته می‌شود ، مجموع پاداش‌های تخفیف‌دار در آینده است. بیایید بازده G t را که از زمان t شروع می‌شود را محاسبه کنیم:

G t = R t + 1 + γ R t + 2 + ⋯ = ∑ k = 0 ∞ γ k R t + k + 1

عامل تخفیف γ ∈ [ ۰ , ۱ ] پاداش‌ها را در آینده جریمه می‌کند، زیرا:

• جوایز آینده ممکن است عدم اطمینان بیشتری داشته باشند. به عنوان مثل، بازار سهام.
• پاداش‌های آینده مزایای فوری را به همراه نمی‌آورند. به عنوان مثال، ما به عنوان یک انسان، ممکن است ترجیح دهیم به جای ۵ سال بعد، امروز تفریح ​​کنیم.
• تخفیف باعث راحتی ریاضی می‌شود. به عنوان مثال، ما برای محاسبه بازده نیازی به پیگیری مراحل آینده برای همیشه نداریم.
• لازم نیست نگران حلقه‌های بی‌نهایت در نمودار انتقال حالت باشیم.

حالت-مقدار یک حالت s بازده مورد انتظار است اگر در زمان t در حالت S t = s باشیم:

V π ( s ) = E π [ G t | S t = s ]

به طور مشابه، ما اقدام-مقدار ("Q-value"؛ Q به عنوان "کیفیت" من معتقدم؟) یک جفت حالت-اقدام را به این صورت تعریف می‌کنیم:

Q π ( s , a ) = E π [ G t | S t = s , A t = a ]

علاوه براین، از آنجایی که ما از خط مشی هدف π پیروی می‌کنیم، می‌توانیم از توزیع احتمال بر روی اقدامات ممکن و مقادیر Q برای بازیابی مقدار حالت استفاده کنیم:

V π ( s ) = ∑ a ∈ A Q π ( s , a ) π ( a | s )

تفاوت بین اقدام-مقدارو حالت-مقدار تابع مزیت اقدام است ("A-value"):

A π ( s , a ) = Q π ( s , a ) − V π ( s )

خط مشی و ارزش بهینه

تابع مقدار بهینه، حداکثر بازده را تولید می‌کند:

V ∗ ( s ) = max π V π ( s ) , Q ∗ ( s , a ) = max π Q π ( s , a )

خط مشی بهینه به توابع ارزش بهینه دست می‌یابد:

π ∗ = arg ⁡ max π V π ( s ) , π ∗ = arg ⁡ max π Q π ( s , a )

و البته داریم

V π ∗ ( s ) = V ∗ ( s ) و Q π ∗ ( s , a ) = Q ∗ ( s , a )